Discrete-Time Hamiltonian Dynamics
… a symplectic-energy-momentum integrator.
Introduction
What is the best way to implement the laws of physics on a computer? Typical implementations of Newton’s law 
Discrete-time Hamiltonian dynamics (DTH dynamics) is a discrete mechanics which exactly conserves energy and linear and angular momentum and has a coordinate-invariant formulation based on a discrete variational principle. To my knowledge, DTH dynamics is the only known example of what is called a symplectic-energy-momentum integrator.
Example (Simple Harmonic Oscillator)
The simple harmonic oscillator is an example of a linear Hamiltonian dynamical system. A spring-mass system and an LC circuit are both simple harmonic oscillators. For such systems, DTH dynamics reduces to the midpoint and trapezoid schemes commonly used to integrate differential equations.
Example (Pendulum)
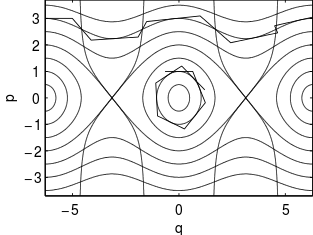A pendulum is one of the simplest examples of a non-linear Hamiltonian dynamical system. The figure to the right is the phase portrait of a pendulum. The piecewise-linear, continuous trajectories in the figure are examples of DTH trajectories.
Background
My work on DTH dynamics originated from my effort to obtain the exact energy and momentum conserving properties of the discrete mechanics of my thesis advisor, Professor Donald Greenspan, from the variational principle used in the discrete mechanics of Nobel Laureate T. D. Lee.
Existence and uniqueness results as well as preliminary work on the coordinate invariance of DTH dynamics is given in my 1992 Ph. D. Thesis. In my 1994 paper, I proved that DTH dynamics is symplectic and hence a symplectic-energy-momentum integrator. I also described points in phase space which appeared to be singularities in DTH dynamics. My 1995 paper explored other ways for using conservation of energy to adapt the step size of the midpoint scheme. In my 1997 paper, I characterized the asymptotic behaviour of time in DTH dynamics.
In my 2005 paper, I explain how to regularize the points described in my 1994 paper in a manner which reserves the symplectic-energy-momentum properties of DTH dynamics. In my 2006 paper, I generalized the existence and uniqueness results given in my 1992 Ph. D. Thesis. In my 2009 paper, I describe efficient iteration schemes for DTH dynamics and demonstrate that even though DTH dynamics is implicit, its adaptive capabilities make it competitive with a widely used explicit scheme – the leap-frog method – for a three-body, near collision, trajectory.
Papers
Discrete-Time Hamiltonian Dynamics, Ph. D. Thesis, U. of Texas at Arlington, 1992.
PDF
Time-Discretization of Hamiltonian Dynamcial Systems, Computers and Mathematics with Applications, 28 (10-12): 123-145, 1994.
PDF
A Variable Time-Step Midpoint Scheme for Hamiltonian Systems, RHIT Mathematics Technical Report, MS TR 95-03, May 1995.
PDF
A Discrete-Time Formulation of Hamiltonian Dynamics, June 28, 1997. (unpublished)
Submitted to Physica D, June 1997. Why symplectic-energy-momentum integration does not violate Ge’s Theorem is explained for the first time in this manuscript! This manuscript was freely shared with Professor Jerrold Marsden during a discussion I had with him after his lecture on discrete mechanics at the IAS/Park City Mathematics Institute’s summer session on Symplectic Geometry and Topology, on July 18, 1997, Park City, Utah, U.S.A. The manuscript predates C. Kane, J. E. Marsden and M. Ortiz announcement of a symplectic-energy-momentum integrator in the Journal of Mathematical Physics, 40, July 1999. The manuscript was updated February 25, 1998 to include a discussion of Professor Ernst Hairer’s meta-algorithm for variable-step symplectic integrators.
PDF (1997)
PDF (1998)
How to Regularize a Symplectic-Energy- Momentum Integrator, arXiv:math/0507483, July 2005.
PDF
Animation of a one parameter family of DTH trajectories crossing 
Is Symplectic-Energy-Momentum Integration Well-Posed? arXiv:math-ph/0608016, August 2006.
PDF
Efficient Symplectic-Energy-Momentum Integration, Proceedings of the 2009 International Conference on Scientific Computing. Las Vegas, Nevada, July 13-16, 2009.
PDF
Animation of a near-collision, three-body trajectory.
- Leap-Frog Method
- DTH Dynamics
Yosi Shibberu 